Como calcular o erro médio absoluto no Excel
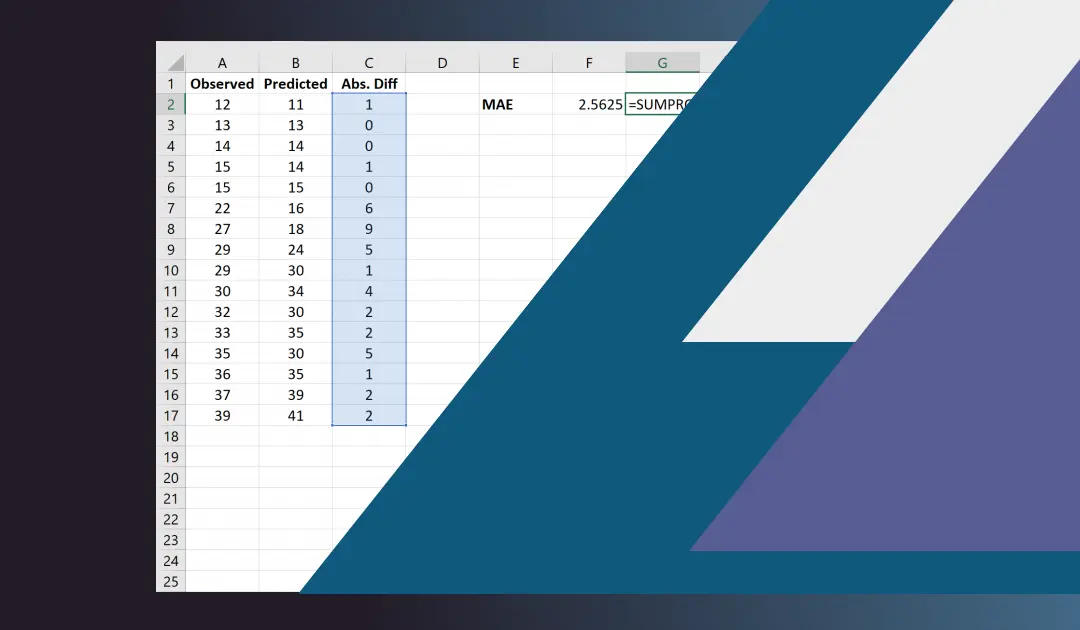
O Erro Médio Absoluto (MAE) é uma métrica amplamente utilizada para medir a precisão de previsões ou modelos estatísticos. Ele calcula a média das diferenças absolutas entre os valores reais e previstos, sendo útil para avaliar o desempenho de um modelo. Abaixo está um guia detalhado sobre como calcular o MAE no Excel:
Índice
1. Estruture sua Tabela de Dados
Antes de começar, organize seus dados em uma tabela com as seguintes colunas:
- Valores Reais: Os valores observados ou medidos.
- Valores Previstos: Os valores estimados ou previstos pelo modelo.
- Erro Absoluto: A diferença absoluta entre os valores reais e previstos.
Exemplo para calcular o erro médio absoluto no Excel
| Valores Reais | Valores Previstos | Erro Absoluto |
|---|---|---|
| 100 | 110 | 10 |
| 200 | 190 | 10 |
| 150 | 160 | 10 |
| 300 | 290 | 10 |
2. Insira os Dados no Excel
- Abra o Excel e insira seus dados nas colunas correspondentes:
- Coloque os "Valores Reais" na coluna A (por exemplo, células A2:A5).
- Coloque os "Valores Previstos" na coluna B (por exemplo, células B2:B5).
3. Calcule o Erro Absoluto
Na terceira coluna (Erro Absoluto), insira a fórmula para calcular a diferença absoluta entre os valores reais e previstos.
Use a função EMA=soma dos erros absolutos + número total de observações
Neste caso:
EMA=10+10+10+104=𝟏𝟎5
Dicas Úteis
Certifique-se de que todas as células estão formatadas corretamente como números.Para grandes conjuntos de dados, use intervalos dinâmicos ou tabelas nomeadas no Excel para facilitar cálculos futuros.
Caso precise comparar vários modelos preditivos, crie colunas adicionais para cada conjunto de previsões e calcule o EMA separadamente.6.
Fórmulas Resumidas
Aqui estão as fórmulas usadas no cálculo do EMA:
Erro Absoluto:
=ABS(A2-B2)Erro Médio Absoluto:
=MÉDIA(C2:Cn)
(Substitua Cn pela última linha do intervalo.)Exemplo Visual Completo no Excel
Tabela Completa: Linha A (Valores Reais) B (Valores Previstos) C (Erro Absoluto)
1 Valores Reais Valores Previstos Erro Absoluto
2100-110 =ABS(A2-B2) → 10
3200-190 =ABS(A3-B3) → 10
4150-160 =ABS(A4-B4) → 10
5300-290 =ABS(A5-B5) → 10
Cálculo Final do EMA:
Na célula D1:
Fórmula:=MÉDIA(C2:C5)
Resultado:EMA = 10
O que é o erro médio absoluto?
O erro médio absoluto (MAE) é uma métrica amplamente utilizada para avaliar o desempenho de modelos de regressão em machine learning e estatística. Ele mede a média das diferenças absolutas entre os valores previstos por um modelo e os valores observados, sem considerar o sinal dessas diferenças. Em outras palavras, o MAE calcula quão longe, em média, as previsões estão dos valores reais.
A fórmula do MAE pode ser expressa matematicamente como:
(MAE = \frac{1}{n} \sum_{i=1}^{n} |y_i - p_i|)
Onde:
- n é o número total de amostras;
- yi representa os valores observados (reais);
- pi são os valores previstos pelo modelo;
- |yi−pi| é o valor absoluto da diferença entre o valor observado e o previsto.
Como funciona na prática?
Para entender melhor, considere um exemplo simples: imagine que você está avaliando um modelo que prevê o consumo de combustível de veículos. Se para um veículo específico o consumo real foi de 12 litros e a previsão do modelo foi de 10 litros, a diferença absoluta seria 2 litros. O MAE seria calculado como a média dessas diferenças absolutas para todas as amostras disponíveis.
Por exemplo:
- Valores reais (y): [10, 12, 15, 8, 8]
- Valores previstos (p): [12, 11, 13, 7, 9]
Os erros absolutos seriam:|10−12|=2,|12−11|=1,|15−13|=2,|8−7|=1,|8−9|=1
A soma dos erros absolutos seria 2+1+2+1+1=7. Dividindo pelo número total de amostras (n=5), temos:MAE=75=1.4
Portanto, neste caso, o MAE indica que as previsões do modelo têm um erro médio absoluto de aproximadamente 1.4 unidades.
Interpretação do MAE
O MAE fornece uma medida intuitiva da precisão do modelo:
- Quanto menor for o valor do MAE, melhor será a performance do modelo.
- Um MAE igual a zero indicaria que as previsões coincidem exatamente com os valores reais.
No entanto, é importante lembrar que ele não diferencia entre erros positivos e negativos (ou seja, superestimações e subestimações), já que utiliza apenas os valores absolutos das diferenças.
Vantagens e limitações
Vantagens:
- Simplicidade: É fácil de calcular e interpretar.
- Robustez: Não dá peso excessivo aos outliers (valores extremos), ao contrário do Erro Quadrático Médio (MSE).
Limitações:
- Não considera proporcionalidade: O mesmo erro absoluto terá impacto idêntico independentemente da escala dos dados. Por exemplo, um erro de “5” pode ser insignificante se os valores reais forem na ordem de milhares mas muito relevante se forem na ordem das dezenas.
Por isso, em alguns casos específicos onde a escala importa mais (como previsões financeiras ou vendas), métricas relativas como MAPE (Erro Médio Absoluto Percentual) podem ser preferidas.